A data set on electoral institutions and the number of political parties; illustrates negligible effects (or equivalence tests) and non-normal residuals
Source:R/cg2006.R
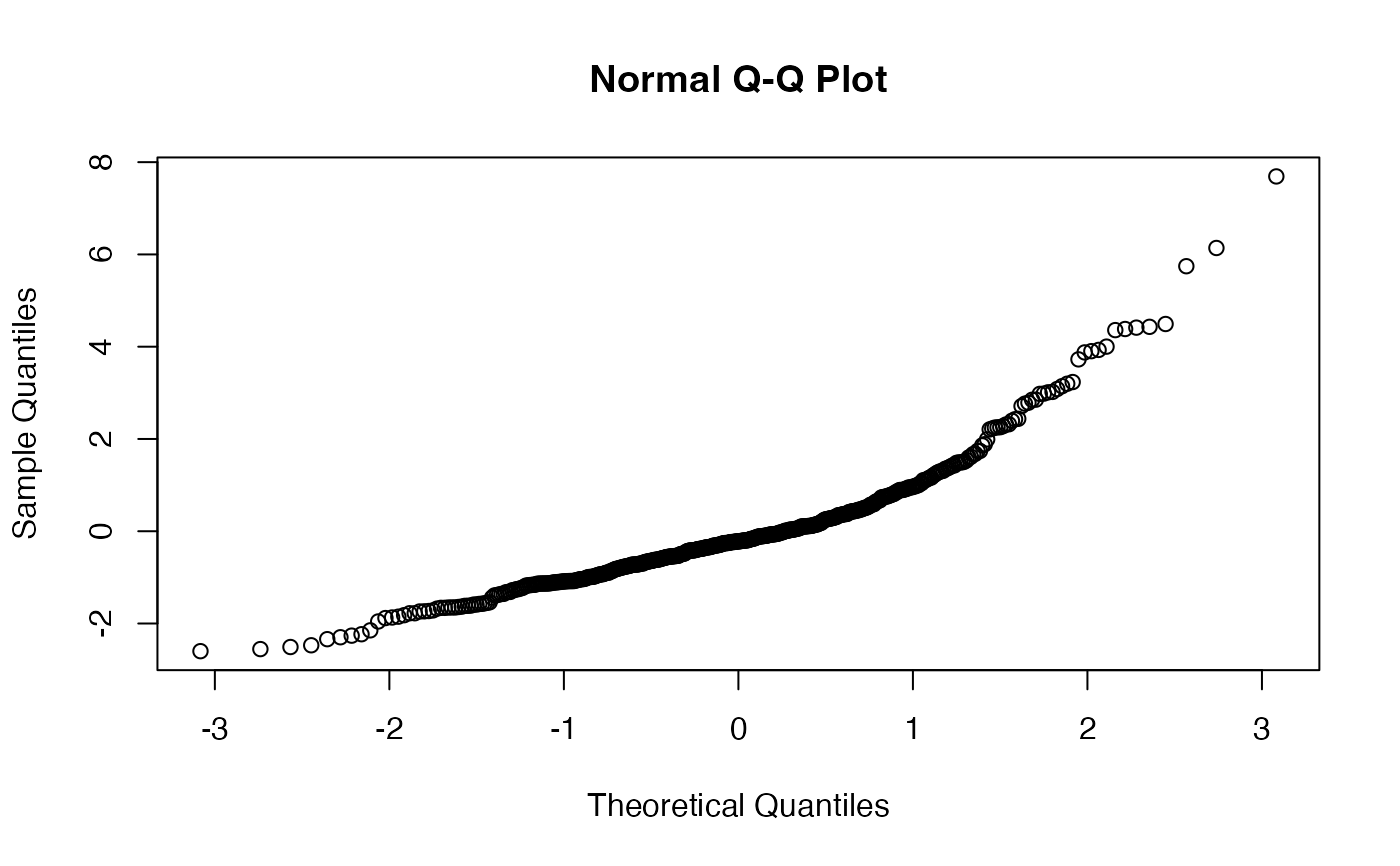
cg2006.RdA data set to reproduce Clark and Golder's "Established Democracies 1946-2000" model in Table 2 on p. 698. I use these data as an example of arguing for a negligible effect or equivalence testing (Rainey 2014) and as an example of regression models with non-normal errors (Baissa and Rainey 2018).
Format
A data frame with 50 observations of rescaled versions of the following 10 variables:
- country
the name of the country that held the election
- year
the year of the election
- average_magnitude
the average of the district magnitude (the number of seats available in the district) across all the districts in the country
- enep
a measure of the effective number of political parties in the system. Calculated as \(ENEP_j = \dfrac{1}{\sum_{i = 1}^n v_{ij}^2}\), where \(ENEP_j\) represents the effective number of electoral parties in election \(j\) and \(v_{ij}\) represents the vote share (as a proportion) for party \(i\) in election \(j\). This particular variable is the effective number of electoral parties once the "other" category has been "corrected" by using the least component method of bounds suggested by Taagepera (1997).
- eneg
a measure of the effective number of ethnic groups in the system. Calculated analogously to ENEP.
- upper_tier
the percentage of all legislative seats allocated in electoral districts above the lowest electoral tier.
- en_pres
a measure of the effective number of presidential candidates. Calculated analogously to ENEP.
- proximity
a measure of the temporal proximity of presidential and legislative elections. Calculated as \(2 \times \lvert \frac{L_t - P_{t - 1}}{P_{t + 1} - P_{t - 1}} - 0.5\rvert\), where \(L_t\) is the year of the legislative election, \(P_{t–1}\) is the year of the previous presidential election, and \(P_{t+1}\) is the year of the next presidential election.
References
Baissa, Daniel K., and Carlisle Rainey. 2018. "When BLUE Is Not Best: Non-Normal Errors and the Linear Model." Political Science Research and Methods 8(1): 136–48. doi:10.1017/psrm.2018.34 .
Clark, William Roberts, and Matt Golder. 2006. "Rehabilitating Duverger’s Theory." Comparative Political Studies 39(6): 679–708. doi:10.1177/0010414005278420 .
Clark, William and Matt Golder. 2007. "Legislative_new.tab." Replication data for: Rehabilitating Duverger's Theory: Testing the Mechanical and Strategic Modifying Effects of Electoral Laws. doi:10.7910/DVN/HGXPHP/SVLIF1 . Harvard Dataverse, V1.
Rainey, Carlisle. 2014. "Arguing for a Negligible Effect." American Journal of Political Science 58(4): 1083–91. doi:10.1111/ajps.12102 .
Rainey, Carlisle. 2013. "cg.csv." Replication data for: Arguing for a Negligible Effect. Harvard Dataverse, V2. doi:10.7910/DVN/23818/TZW36U .
Examples
# a simple example
# load Clark and Golder's data
cg <- crdata::cg2006
# reproduce Clark and Golder's 1946-2000 Established Democracies model in Table 2 on p. 698
f <- enep ~ eneg*log(average_magnitude) + eneg*upper_tier + en_pres*proximity
fit <- lm(f, data = cg)
summary(fit)
#>
#> Call:
#> lm(formula = f, data = cg)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -2.5997 -0.7910 -0.2183 0.4440 7.6906
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 2.91571 0.17559 16.605 < 2e-16 ***
#> eneg 0.11160 0.07139 1.563 0.118653
#> log(average_magnitude) 0.07799 0.11587 0.673 0.501240
#> upper_tier -0.05655 0.02018 -2.803 0.005276 **
#> en_pres 0.26385 0.06430 4.103 4.79e-05 ***
#> proximity -3.09757 0.35236 -8.791 < 2e-16 ***
#> eneg:log(average_magnitude) 0.26366 0.06735 3.915 0.000104 ***
#> eneg:upper_tier 0.05919 0.01429 4.141 4.08e-05 ***
#> en_pres:proximity 0.68317 0.13730 4.976 9.08e-07 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 1.332 on 478 degrees of freedom
#> Multiple R-squared: 0.3966, Adjusted R-squared: 0.3865
#> F-statistic: 39.28 on 8 and 478 DF, p-value: < 2.2e-16
#>
# QQ-plot of residuals
qqnorm(residuals(fit))